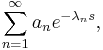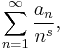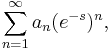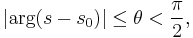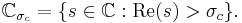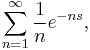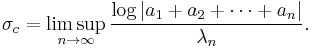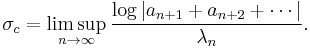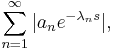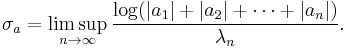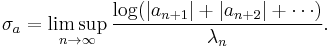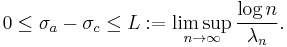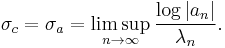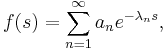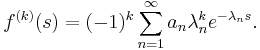General Dirichlet series
In the field of mathematical analysis, a general Dirichlet series is an infinite series that takes the form of
where 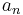 ,
,  are complex numbers and
are complex numbers and 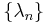 is a strictly increasing sequence of positive numbers tends to infinity (1).
is a strictly increasing sequence of positive numbers tends to infinity (1).
A simple observation shows that an 'ordinary' Dirichlet series
is obtained by substituting 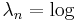 n while a power series
n while a power series
is obtained when 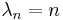 .
.
Contents |
Fundamental theorems
If a Dirichlet series is convergent at 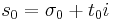 , then it is uniformly convergent in the domain
, then it is uniformly convergent in the domain
and convergent for any 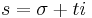 where
where  .
.
There are now three possibilities regarding the convergence of a Dirichlet series, i.e. it may converge for all, for none or for some values of s. In the latter case, there exist a 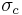 such that the series is convergent for
such that the series is convergent for  and divergent for
and divergent for 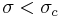 . By convention,
. By convention, 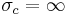 if the series converges nowhere and
if the series converges nowhere and 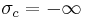 if the series converges everywhere on the complex plane.
if the series converges everywhere on the complex plane.
Abscissa of convergence
The abscissa of convergence of a Dirichlet series can be defined as 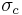 above. Another equivalent definition is
above. Another equivalent definition is
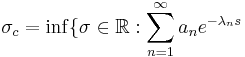 converges for any s where Re(s)>
converges for any s where Re(s)>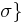 .
.
The line 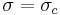 is called the line of convergence. The half-plane of convergence is defined as
is called the line of convergence. The half-plane of convergence is defined as
The abscissa, line and half-plane of convergence of a Dirichlet series are analogous to radius, boundary and disk of convergence of a power series.
On the line of convergence, the question of convergence remains open as in the case of power series. However, if a Dirichlet series converges and diverges at different points on the same vertical line, then this line must be the line of convergence. The proof is implicit in the definition of abscissa of convergence. An example would be the series
which converges at 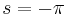 i (alternating harmonic series) and diverges at
i (alternating harmonic series) and diverges at 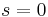 (harmonic series). Thus,
(harmonic series). Thus, 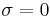 is the line of convergence.
is the line of convergence.
Suppose that a Dirichlet series does not converge at 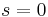 , then it is clear that
, then it is clear that 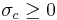 and
and 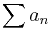 diverges. On the other hand, if a Dirichlet series converges at
diverges. On the other hand, if a Dirichlet series converges at 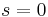 , then
, then 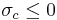 and
and 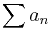 converges. Thus, there are two formulas to compute
converges. Thus, there are two formulas to compute 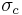 , depending on the convergence of
, depending on the convergence of 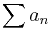 which can be determined by various convergence tests. These formulas are similar to the Cauchy-Hadamard theorem for the radius of convergence of a power series.
which can be determined by various convergence tests. These formulas are similar to the Cauchy-Hadamard theorem for the radius of convergence of a power series.
If 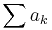 is divergent, i.e.
is divergent, i.e. 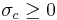 , then
, then 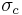 is given by
is given by
If 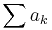 is convergent, i.e.
is convergent, i.e. 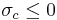 , then
, then 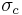 is given by
is given by
Abscissa of absolute convergence
A Dirichlet series is absolutely convergent if the series
is convergent. As usual, an absolutely convergent Dirichlet series is convergent, but the converse is not always true.
If a Dirichlet series is absolutely convergent at 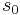 , then it is absolutely convergent for all s where
, then it is absolutely convergent for all s where 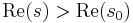 . A Dirichlet series may converge absolutely for all, for no or for some values of s. In the latter case, there exist a
. A Dirichlet series may converge absolutely for all, for no or for some values of s. In the latter case, there exist a 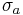 such that the series converges absolutely for
such that the series converges absolutely for 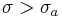 and converges non-absolutely for
and converges non-absolutely for 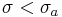 .
.
The abscissa of absolute convergence can be defined as 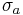 above, or equivalently as
above, or equivalently as
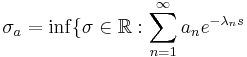 converges absolutely for any s where Re(s)>
converges absolutely for any s where Re(s)>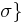 .
.
The line and half-plane of absolute convergence can be defined similarly. There are also two formulas to compute 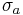 .
.
If 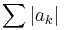 is divergent, then
is divergent, then 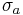 is given by
is given by
If 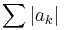 is convergent, then
is convergent, then 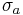 is given by
is given by
In general, the abscissa of convergence does not coincide with abscissa of absolute convergence. Thus, there might be a strip between the line of convergence and absolute convergence where a Dirichlet series is conditionally convergent. The width of this strip is given by
In the case where L= 0, then
All the formulas provided so far still hold true for 'ordinary' Dirichlet series by substituting 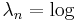 n.
n.
Analytic functions
A function represented by a Dirichlet series
is analytic on the half-plane of convergence. Moreover, for 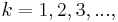
Further generalizations
A Dirichlet series can be further generalized to multi-variables case where 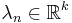 , k = 2, 3, 4,..., or complex variable case where
, k = 2, 3, 4,..., or complex variable case where 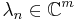 , m = 1, 2, 3,...
, m = 1, 2, 3,...
References
- G. H. Hardy, and M. Riesz, The general theory of Dirichlet's series, Cambridge University Press, first edition, 1915.
- E. C. Titchmarsh, The theory of functions, Oxford University Press, second edition, 1939.
- Tom Apostol, Modular functions and Dirichlet series in number theory, Springer, second edition, 1990.
- A.F. Leont'ev, Entire functions and series of exponentials (in Russian), Nauka, first edition, 1982.
- A.I. Markushevich, Theory of functions of a complex variables (translated from Russian), Chelsea Publishing Company, second edition, 1977.
External links
- Hazewinkel, Michiel, ed. (2001), "Dirichlet series", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=d/d032920